Twittermeldingen til Walty Walt har fått over 20 000 likes og mer enn 3000 retweets. Meldingen hans er like enkel som overskriften på denne saken. Etter en liten runde blant venner viser det seg at det er flere svar på dette spørsmålet enn man skulle tro.
Vi bryr nok hjernen vår mindre og mindre med regning fordi vi alle går med en kraftig kalkulator i form av mobiltelefon i lommen. Men av og til tar man snarveien om god gammeldags hoderegning. Og da viser det seg at vi har mange forskjellige metoder.
Jeg har alltid vært fascinert av den japanske og meget visuelle metoden for multiplikasjon, men den krever papir og blyant.
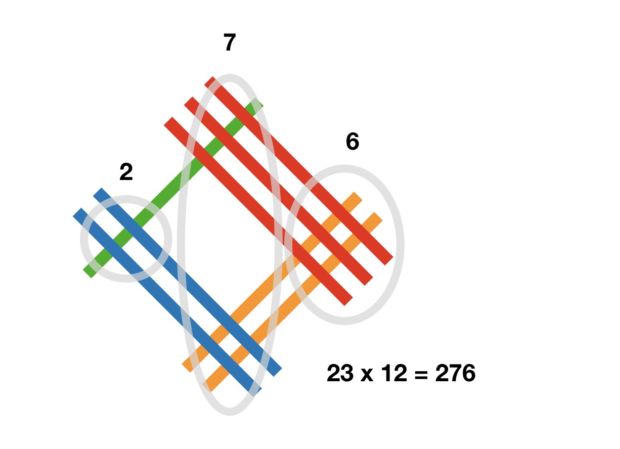
Når man stokker tall i hodet driver man også fort med forskjellige former for visualisering og forenkling. For regnestykket i tittelen her er jeg en soleklar 25 + 50. Og tenker at det er den eneste fornuftige måten å se dette regnestykket for seg.
Om litt vil kommentarfeltet her vise at jeg tar fullstendig feil. Hvordan tenker dere?
Automatisert nyhetsbrev fra NRKbeta
Få et ping i postkassa hver gang vi publiserer noe interessant om teknologi eller medier!
Jeg vil ikke si at det er feil selv om jeg tenker annerledes. Jeg ser 20+40+14+1 😀
Hm, jeg velger 20+40+15.
((2+4)x10+(7+8)=75
Jeg tenkte umiddelbart 25 + 50.
Jeg tenkte med en gang 2+4 (eller 20+40)=60 + 15(8+7)=75
Kalkulatoren på iPhone er jammen god å ha…..
tenkte jeg.
Jeg ser 50+27-2
27+50-2=75
48+30 – 3= 75
27+48
Jeg tar
20+40
5+5
2+3
Jeg slenger meg på her!
Jeg samler opp tierne først, altså 20+40= 60
Så tar jeg resten, som jeg regner ut som 7+7=14 og legg til 1.
Altså 60 + 14 + 1 =
60 + 15 =
75
8+7 = 15, 20 + 40 = 60 = 75
7+8
2+4+1
=75
27+48
30+48=78-3=75
Enkelt og greit 😊
30+50-5=75
Runder begge av oppover, trekker fra det som mangler på hele tiere.
7 + 48 = 55 + 20 = 75 👍🏻
Hjerner er forskjellige😃 Jeg ser 48+20+7
Jeg tar 2 i fra 27 og legger til 48 = 50 + 25 = 75
30+48=78
78-3=75
Jeg tenkte slik: Altså å sette opp regnestykket slik jeg lærte på barneskolen. Starter med 27 øverst, så 48 under, med + foran, så med en strek under. Så = under +, men under streken, så regner jeg 7+8=15, altså 5 under streken på enerplassen. 1-tallet står i mente over 2 og 4 på tierplassen, og må legges sammen med 2 og 4, og da blir det 1+2+4=7, som settes ved siden av 5-tallet på på tierplassen under streken. Altså et enkelt plusstykke med mente på tierplassen når det legges sammen. Enkel barneskoleregning😉
(48+2)+25
Gutten min på 8 år velger:
20+48=68
68+2=70
70+5=75
Mamma’n velger:
8+7=15
20+40=60
60+15=75
Jeg regner slik:
7+8 =
8+8 = 16 -1 = 15
Husker 5eren og 1 ekstra tier og regner slik:
1+2+4=7 = 70
= 75
Det jeg tenker er 68+7… 20+48 er tall som bare kommer uten tenking…
Jeg kjører Ingrid sin metode. 48+7=55+20=75
Tenker med en gang:
(8+7)+(20+40)=75
Æ ser 7+8 e 15, så 20+40 e 60 å da e d jo 75 som e svaret.
27+48
Starter med 60
Så
7+8= mer enn en tier, tar tieren ut
(7+3). Sitter igjen med en 5-er fra 8.
Da blir det
60+10+5
48 pluss 7 pluss 20
48 + 20 = 68 + 7 = 75.
7 +8 = 15 , så 2 + 4 (20 + 40) = 60 altså 15 + 60 = 75
Jeg ser helt klart 15+60=75, gøy at det finnes så mange ulike mattehoder😎
(20+40)+(8+7)
7+7=14+1=15
20+40=60+15=75
2*7=14
14-((8-7)*10)=4
27+48
Tenker akkurat som deg:25+50
27+8= 35 35+40=75
✌️
Jeg tenkte først at 7 +8 er 15 Og plusset på 60.
I første øyekast 8+7=15+60=75
Med en gang etter jeg har sagt 75=25+50
Runder oppover 50+30 = 80-5
som mangler til hele tiere = 75.
Jeg ser 68+7=75
20+40 = 60
8+8 = 16-1 = 15
60+15 = 75
Hvorfor dille så? Denne addisjonen er for enkel til å dele opp i alskens deler: 27+48=
8+7=15, dvs 5 og 1 i mente til 2+4 = 75
25 + 50 = 75
Presis avrundet
20+40….+7+8!
Eg tenkte slik når eg såg 27+48:
20+40=60
60+7=67
Kva er tiarvennen til 7? Jo 3.
(Då er eg komt til 70)
Så tok eg 8-3=5, som då blei einarplassen.
Altså 75.
Eg innser dette var vanskelig tenkt når eg ser
Andre løysingar i kommentarfeltet,
men spørsmålet var jo korleis eg tenkte 😉
20+40+15
Jeg har liten rspekt for denne mannen og tenker at dette er en høyst politisk måyeå komme fram til 75 på.
27 + 48 = 75.
Utregnet slik:
7 + 8 = 15
20 + 40 = 60
60 +15 = 75
Matte er gøy🤪
Matte er bra for hode
20+40=60
7+8=15
=75
Jeg tenker på samme måte.
Enig
Helt likt her også!
Akkurat samme her
Samme
Umiddelbart gjorde jeg det samme og det gikk lynraskt, ett blikk og så var det 75!
Ditto
Helt enig – logisk oppdeling og så legge sammen
Samme her.
Vi regner likt!
Ja,det skjer i mitt hode,og
Tenker 27 + 40 = 67, + 8 = 75….
Slik regner jeg også.
Slik tenker jeg og.
Akkurat samme tenkemåte her 😁
Jeg gjør det samme
samme her
Jepp, helt likt her.
Samme her
Enig – sånn er det jo!
Enig, dette er også min strategi 🙂
jeg har samme tenkemåte !
Samme her
Samme her.
Samme her
20+40 så 7+8
Gjør det på akkurat samme måte, uansett hvor store tall plusser jeg 10ere/100ere/1000, for så å samle alt mindre til hele tiere og slenge det også på.. Mulig det høres tungt ut, men jeg er lynkjapp i hoderegning og tar skjeldent feil så det funker for meg!👏🏽👏🏽
Yes
Enig!
Samme gjør jeg 😀
Jeg tenker likt… 20+40+8+7
Samme
Samme metode bruker jeg.
Enig, bare omvendt, begynner med enerne: 15+60
Gjør akkurat på samme måte og har alltid gjort det, uansett tall.
Gjør det samme, men sier «seksti» inni hodet mitt mens jeg gjør det. Hvis ikke er det fare for at jeg blir usikker på om 60 er før eller etter at jeg har lagt til tieren i 15.
Jepp!
Er også en soleklar 60+15 her (7+8+20+40)
Me 2
Mest logisk for meg også!
Jeg tenker akkurat slik jeg også 😄
Enig, gjør akkurat det samme, automatisk.
Samme.
7+8 smelter sammen som 15 og blir lagt oppå en tykk 2+4 som er 60. Det skjer med et blikk «samtidig.
Ja, tenkte (20+40) 60 + (7+8) 15 =75
Nett slik jeg også gjør det. Hjernen har svaret før jeg nærmest rekker å reflektere om hvorvidt det er korrekt.
Jeg må også si meg enig her, legger først sammen enerne, så tierne, og så legges alt sammen, 15+60=75.
27+40 = 67 +8 = 75
Summerer tierne og legger til summen av enerne
7+8=15
2+4=6
_______
= 75
Samme som forfatteren. Jeg flytter over to fra 27 til 48 får å få sistnevnte til å bli 50, og legger de sammen med de resterende 25.
30+45=75
Jepp
Helt identisk 😉
20+48=68
68+7=75
«Flere veier til rom»
Tenker som jeg ville skrevet utregningen:
7+8=15. 5 og«en i mente» som vi sa på 60-tallet. 2+4+1=7. 75 mange veier til rom ja.
Tenkwr likt som deg her
Samme som Henrik 🙂
Eller lån fra en side til en annen;
f.eks. tar jeg 3 fra høyre og ser 30 + 45 = 75
samme her, dersom vi visualiserer og leker litt med tallene tror jeg vi regner raskere enn de som gjør det «etter boka» men det krever kanskje litt mere ..cpu 😀
Samme her; jeg låner fra siste del av stykket til første del, slik at første del blir en hel tier (30). Så legger jeg på det som står igjen (45).
Ja, det er det enkleste 🙂
30 + 45 = 75.
Eller (27 + 3) + (48 – 3)
Helt klart tierne først og så enerne, som Martin Haugen skriver.
20+40=60
7+8=15
60+15=75
Quick maffs
Slik tenker jeg òg.
27+8+40=75
Akkurat slik tenker jeg også:)
27+48 = 20+55 = 75
Endelig fant jeg en som tenker på samme måte som meg!
Enig. Dvs at 55 kommer ved å ta 48 + 7 først. Men det skjer nesten uten å tenke over det.
Min løsning også: 48+7=55+20=75
7+48=55
20+55=75
Ser at denne er noe kronglete.
Gjorde sammen. Godt jeg ikke var aleine.
Endelig! Samme her.
Kjæresten min er mattelærer og gjorde det samme. Måtte overraskende langt for å komme til denne fremgangsmåten.
Ikke kronglete i det hele tatt, falt rett inn i mitt tjukke hode 🙂
27 + 48 =
27 + 8 + 40 =
35 + 40 =
75
23×10 + 23×2 = 230 + 46 = 276
Begynner bakerst og tar «enerene» (barneskolelærdom som sitter i ryggmargen…), altså 7+8=15 først, så 2+4=6, tar med tieren fra 15 og får 7 og så hadde jeg femmeren igjen på enerplass… Høres mye mer tungvint ut når jeg skriver det ned, det gikk ganske fort i hodet, lover… 😉
Ser du var akkurat før meg med samme forklaring, gikk visst saktere hos meg 😅
15+60 =75, ja. Opplagt løsning
Samme her, går fort i hue
For meg blir det er mønster å gjøre det slik😁
Samme her. Einarane først og så tiarane.
Her også. Som på barneskolen; enerene først, tar med tieren over til tierplassen.
Stiller meg bak denne 🙂 Går fort i hodet!
Jeg ser 27+48=75.
Benytter nok andre ‘indirekte’ metoder hvis det er mer komplisert.
Heilt enig!
Jess for f…! Ble nesten redd for at jeg ikke fant det her! Hva er det de driver med? 😀
Slik fjørjeg, også. Såpass enkelt så ser jeg barepå tallene og finner svaret uten å tenke noe overdette.
For i tiden, den gang en kjøpte varer over disk i butikken, og «ingen» varer kostet x,99 gav dette også en «liten pjokk» utfordringen å komme frem til resultatet før butikkdamen hadde lagt sammen tallene. Og denne «utfordringen» har nok fulgt meg siden, – sammen med erfaringen.
Jeg har en hobby som innebærer masse hoderegning, så jeg veit også umiddelbart at det er 75.
Først 10-erne og så 1-erne
Skulle ønske jeg hadde noen av de svarene over. Men for meg blir det tilbake til barneskolen og så setter jeg dem oppå hverandre. 7+8=15. Flytter tieren over slik at det blir 1+2+4=7. Og dette gjøres tungvint og tregt oppi hodet 🙊
27
+48
75
20 + 40 +7 +8 =75
2+4=6 7+8=15 60+15 =75. Synes det er enklest å fjerne 0
Det gjør jeg også
15+60!
Umiddelbart legger jeg sammen 2+4 tiere og legger til 7+8 = 15 og håper at jeg kommer på hva jeg kom fram til først. Så kontrollregner jeg med 7+8 + 20 + 40 og ser oversiktlig at det er 75.
Det er lettere om det går automatisk.
Det første som slår meg er:
48 + 30 -3 = 75
Sjæl😄👌
Samme her. Men hadde 48 stått først ville det blitt 50+27-2.
Samme her👍
Gjør også som Ivar (og Terje).
27 + 50, så minus to
Jammen måtte jeg rulle langt ned for å finne en «likesinnet»:
Samme her: Først 27 + 50 = 77 og så – 2 = 75.
Avrunding og faktorisering er nyttige verktøy i min matematiske verktøykasse. Det er nok ikke de mest effektive, og noen ganger ikke presise nok, men de får stort sett jobben gjort.
Til mer avansert matte bruker jeg hjelpemidler, som regel regneark eller stack-baserte kalkulatorer.
Savner min gamle HP 48GX som jeg brukte på høyskolen. 😉
Man får apper som emulerer HP kalkulator med RPN og Enter-tast til de fleste smarttelefoner og nettbrett.
Kan man RPN så føles standard kalkulatorer simple og begrensende.
hvis du først har hatt en HP kalkulator tenker du alltid 48 enter 27 +. 😍
Hvis du brukte en GX så er det ikke så lenge siden du var på høgskole/universitet.
Selv har jeg fremdele HP48SX kalkulatoren i daglig drift.
PS du finner både SX og GX app for Android (vet ikke om det gjelder iPhone)
Som svar på oppgaven tar jeg 7 og hiver på 48 og får 55, deretter legges 20 til.
Først det bakerste:8+7=15 –>5
Så det første: 2+4 og +1 ekstra(fra 15)–>7
Er eg den eneste som bare «ser» 75 automatisk?
Nei 🙈
Nei! Og helt ufattelig for meg hvor vanskelig de fleste gjør dette.
Nei, samme her, dette er lave tall, men folk skal gjøre det så komplisert.
27+40+8
Her er jeg og. 27+40=67+8=75
Endelig noen som tenker som meg👍😁
Endelig en til som går «rett frem! 🙂
Jeg har samme fremgangsmåte. Noen andre svarer at «de bare ser» svaret. Det klarer ikke jeg med 27+48, men jeg klarer det med 27+40=67, så jeg starter der umiddelbart, før jeg begynner å tenke mer bevisst hvordan jeg skal løse resten.
Det gjør nok at jeg bruker lenger tid enn dem som har en strategi fra starten av.
Enerne først, så tiere, hundrer osv.
7+8 = 15
20+40 = 60
60+15 = 75
Problemet jeg ser med å starte «big endian» (store tall først) er om tallene har ulike antall sifre.. f.eks et er noen hundre mens det andre er noen titalls… YMMV 🙂
27+48 blir enklere om jeg tenker/ visualiserer 30+48=78 78-3=75
48+20+7
48+7+20
48 + 7 = 55
55 + 20 = 75
Overrasket over at jeg måtte så langt ned for å finne en likesinnet, men glad det var selveste Einstein.
Eg og
Eg og
Der kom endelig min variant
Yes. Jeg også.
Samme her 🙂 Alltid hoderegnet sånn, og det går ganske raskt synes jeg.
20+40=60
7+8=15
=75
i 20 + 40 plusser jeg egentlig 2 + 4 og henger på den ignorerte 0-en til slutt. 60.
i 8 + 7, så stresser den litt fordi den krysser 10. Da låner jeg 2 fra 7-eren for at 8-eren skal bli 10, så plusser jeg 10 med 5. Av en eller annen grunn så synes jeg litt synd på 5-eren, fordi den var egentlig en 7-er som blei robba. Rart å blande følelser, men jeg kjenner det.
Så 60 + 15 = 75.
Ja til empatisk matte! Vet at noen sjakkspillere mener man skal «snakke» med brikkene og «spørre» dem om de føler de står godt der de står, eller om de bør flyttes på. Kanskje lignende metoder bør innføres i mattefaget?
Deler opp 27 + 48 i enere, tiere osv.
7 + 8 = 15
legger tieren(e) i neste rekke, slik at eg står igjen med 5 i ener rekka
1x + 2x + 4x = 7x
Nå blir rekkefølgen 7 i tieren og 5 i ener rekka, som igjen blir 75
30+50=80
3+2=5
80-5=75
Samme her.
Samme her
Endelig en som tenker som meg…:-)
Samme her.
Jepp.Samme her.
Siden det var kortere vei å runde opp, ble det sånn for meg:
27 + 48 =
(30 + 50) – (3 + 2) =
80 – 5 = 75
Samme som meg 🙂
Og som meg:)
Mitt hue sier: 48+7=55, og 55+20=75
Men er dørgende enig i at den japanske metoden er langt bedre.
Den er jo ikke bedre i det hele tatt. Den er faktisk dårligere. 23×12 går noenlunde bra, men prøv deg på 78×95, og se om det egentlig er så mye lettere. Eller gang sammen to firesifrede tall, og se om du enkelt klarer å holde orden på hvilke krysninger som hører til hvor. For å ikke snakke om all den plassen det tar på papiret.
Det er faktisk akkurat den samme algoritmen som den de fleste av oss har lært på skolen. At et slikt triks allikevel kan spres som noe revolusjonerende (har sett folk være begeistret for dette på facebook flere ganger), synes jeg sier sitt om matteforståelsen ute i befolkningen. Den grafiske fremstillingen har også noen åpenbare svakheter det øyeblikket ting blir litt mer komplisert.
30+50-5=75
Samme her.
Jeg legger til 3 og trekker 3 fra resultatet:
30 + 48 = 78
78 – 3 = 75
Endelig fant jeg én som tenker slik som jeg selv….
7+8=15
20+40=60
60+15=75
Litt kronglete, men blir da rett!
48+7= 55
55+20=75
Jeg har farge-synestesti (se en.wikipedia.org/wiki/Synesthesia#Grapheme-color_synesthesia) og ser derfor rød-gul + grønn-brun.
Synestesi gir den fordelen at jeg har lett for å huske tall. Ulempen er at jeg ikke vektlegger størrelsesordenen.
Alle disse likningene ser tilnærmet like ut for meg:
27 + 48
270 + 48
27 + 480 000
rød-gul(-blank) + grønn-brun(-blank), så det kan gi folk med fargesynestesi en ulempe ved hoderegning.
20+40=60
2+8=70
+ 5 i rest = 75
Men så datt jeg også ut av matte ca. midt i barneskolen.
😂😂😂😂😂 Det forstår jeg at du gjorde! 😂😂👏🏾👏🏾
20+40=60
10-8=2 og her beholder jeg tieren
7-2=5
60+10+5=75
27 + 50 – 2
27+48 regner jeg sammen slik:
20+40=60
60+8+2=70
70+5=75
27+48 regner jeg sammen slik:
20+40=60
60+8+2=70
70+5=75
Akkurat dette eksempelet er så enkelt at det er som at 5 + 3 = 8. Hvordan vet jeg det? Nei… det bare er sånn. 48 + 27 = 75 på samme måte. Jeg er vant med hoderegning – antar at mobilen min har kalkulator, men kan ikke huske å ha brukt den noen sinne.
For mer kompliserte ting avhenger mye av om jeg må ha et eksakt svar. I så fall går jeg fra enere, mente til tiere, mente til hundre osv. Som regel behøver jeg bare et overslag, f.eks. sluttebeløpet på kassalappen på Rema. Ved overslag går jeg andre veien, fra største enhet og nedover. Får jeg mente fra tierne korrigerer jeg den første verdien jeg hadde for hundrerne, og tilsvarende mente fra enerene til tierne (hvis det er behov for et så nøyaktig overslag, da).
Jeg har faktisk oppdaget feil på kassalappen et antall ganger på den måten, men det er mange år siden sist det var til min fordel :-). Det vanlige er at en sixpack har blitt registrert som én boks, og jeg kunne fått fem bokser på kjøpet om jeg ikke hadde gjort oppmerksom på det. Jeg er alltid «dum nok» til at jeg sier ifra.
Ser for meg stykket som jeg ville satt det opp på ark som på ungdomsskolen.
7+8=15, siste siffer blir 5.
1 i minne pluss 2 pluss 5 er 7.
Svaret er 75.
2 + 4 = 6, 7 + 8 = 15, 15 = 1 + 6 og 5 i rest = 7 og 5 = 75.
20+40=60
7+8=15
60+15=75
27+48
40+20=60 + 8 = 68
68 + 2 = 70 + 5 = 75
Ser av en eller annen grunn for meg tall under 10 som en slags terning man kan telle på, eks. 7
et i hodet mitt:
* *
* *
* *
*
30 + 48 = 78 (minus 3) = 75
30 + 50 – 3 – 2
Samme her!
30+50 -5
En engelsk bok som heter «Learn Street Math» er å anbefale dersom man vil lære seg gode hoderegningsteknikker. Ellers er det vel masse øvelse i mønstergjenkjenning som gjelder.
books.apple.com/no/book/learn-street-math/id496694971
Jeg tenker paa en maase 😀
7+48=55+20=75
20 + 40 + 15 = 75
«75,hva betyr det?», var mitt spørsmål. Skjønte først etterpå hva det gjaldt. Hvordan tallet kom vet jeg ikke.
15+60=75
Den japanske metoden for multiplikasjon har jeg aldri helt forstått. Som guttunge lærte jeg derimot fra Det Bestes «Den nye juniorboken» (fra en gang på 60-tallet) å gjøre det binært – men jeg måtte bli datamann for å forstå at det var det som skjedde.
Ta f.eks. 15×13. Trinn for trinn halverer du høyresiden (dropp «og en halv») og dobler venstresiden. Partall i høyre kolonne bringer ulykke, så dem stryker du, sammen med tallet i venstrekolonnen. Adder venstrekolonnen, og du har produktet:
15 – 13
30 – 6 … partall, hele linja strykes
60 – 3
120 – 1
Summer 15 + 60 + 120 = 195.
Slik vi tradisjonelt gjør det:
(Dette blir sikkert skjevt fordi mellomrom blir smalere enn siffer når det vises i innlegget):
15 × 13 =
45 (dvs. 3×15)
15 (10×15, skrevet som 1×15 ett siffer til venstre).
Vi adderer 45+150, og får svaret.
Når vi tar multiplikator-sifrene fra høyre, kan vi se det som å dele på 10 (ikke på 2), og kun se på siste siffer. Er det 0, blir den tilsvarende delsummen 0, den «strykes».
Binærform: Å flytte en delsum ett siffer mot venstre er ikke tidobling men dobling (venstrekolonnen!) Halvering i høyrekolonna er å flytte ett binærsiffer mot venstre. Et partall har 0 som siste siffer, multipliserer vi 1111 med 0, skal det ikke med i summen; det strykes:
1111 × 1101
1111
0000 (0×1111, 1 bit til venstre, strykes)
1111 (1×1111, 2 bit til venstre)
1111 (1×1111, 2 bit til venstre)
Binær addisjon av delsummene: 1111 + 11100 + 1111000 = 11000011
Eller desimalt bit for bit: 128 + 64 + 2 + 1 = 195.
Ifølge Den nye juniorboken kunne disse asiatiske steppefolkene som bruker metoden overhodet ikke forklare hvorfor den fungerer. Vi kan være ganske sikre på at de ikke har lært den fra moderne datamaskiner 🙂
Ooops – alle mellomrommene til venstre forsvant! Javel da må du mentalt forskyve linjene til de blir plassert slik som vi gjorde på barneskolen…
8 + 7 = 15
2 + 4 = 6
60 + 15 = 75
20 + 40 + (2×8) – 1 = 75
Etter mange år med programmering og aktiv bruk av å tenke på 1/2/4/8/16/32 etc er jeg såpass yrkesskadet at 7+8 instinktivt leses som 8+8-1 😛
30+50-(3+2) tenker jeg.
Det første jeg tenkte var 48+7=55+20=75
Hvis jeg skal addere to tall, legger jeg alltid sammen fra venstre, og tar hensyn til om tallene rett til høyre blir over eller under ti.
4 + 2 + 1 = 7 (over 10 til høyre)
8 + 7 = 5 (tieren er allerede brukt opp, den gidder jeg ikke se for meg)
Svar: 75
Jeg tenker også sånn. Registrerer først ved et blikk at 8+7 blir over 10, og tenker da 4+2, og bare merker meg at vi lander på 70-tallet istedenfor 60. Så legger jeg sammen 8+7, og bare dropper 10-ern derfra.
Først gjorde jeg 20+40=60. Deretter 8+7=15, også 60+15=75.
Tilslutt så jeg at det ikke var noe likhetstegn, og gikk videre.
Tar automatisk enerne først og så tierne, uten å tenke over det:
7+8=15
20+40= 60
60+15=75
Men egentlig synes jeg at journalistens tenkemåte er enklere 🙂
Gjør akkurat det samme som deg!
20+55
Jeg tenker at dette var interessante tall:
3*3^2 + 3*4^2 = 3*5^2
Spennende 😊 kanskje vi kan forenkle addisjon ved å gå via pytagoreiske tripler 😉
Dama er 27, mannen er 48. Det var min første tanke 🙂
Dernest, etter å ha skjønt at det «bare» handlet om matte, 20+40=60.
60+8=68.
68+7 er det samme som 68+2+5,
altså 70+5=75
Hmm, jeg tenker at det blir seksti-femten, altså 75. Uten at jeg egentlig må regne på det.
Da tenker du på fransk: soixante-quinze.
soixante-quince, beklager knefall for autokorrekturen
7+48=55+20=75
Jeg ser absolutt ingenting i hodet mitt av det regnestykket. Jeg får bare hodepine, og så legger jeg hodet under puten og gråter.
20+40+7+8 / 20+40 + 15.
Jeg tar enerne fra første tall og legger til site tall, så tierne.
27+48 => 20+55 = 75
Gjør det samme om det er flere tall
12+84+96 => 10+80+102 = 192
27+48 (48+7=55+20=75)
Den japanske multiplikasjonsmetoden er NØYAKTIG den samme som vi nordmenn lærer på skolen. Bare sett opp gangestykket, regn det ut som du har lært.
Nå har du, mest sannsynlig, i en eller annen rekkefølge regnet ut 3×2, 2×2, 3×1 og 2×1, og lagt dem sammen i kolonner. Ser du på tegningen, så er det 2×1 krysninger til høyre, 2×2 + 3×1 krysninger i midten, og 3×2 krysninger til venstre. Virker prosessen kjent?
Denne metoden får også litt problemer med en gang det er flere enn 9 krysninger til høyre eller i midten. Og skal du ha tre eller flere sifre, så blir det vanskelig å se hvilke grupper med krysninger som hører sammen.
Ingenting revolusjonerende, med andre ord, og litt avhengig av at du er heldig med stykket ditt.
Hey Siri, add 27 to 48 😉
(30+50)-(3+2), runder til nærmeste tiere og trekker fra differansen.
Æ ser 7+8=15
15+20+40=75
Selv tenker jeg 7+8…7+7=14+1=15. 20+55=75
Jeg ser 2+4=6 7+8=15 og så 6+1=7 for så å sette tallene sammen til 75.
Vanskelig å sette ord på en visualiseringsprosess som foregår inne i hodet. Jeg holder alle sifrene på tallplassen sin, tenk tilbake til barneskolen der du skulle sette enerne på enerplassen og tierene på tierplassen osv. Gjør dette systematisk i hodet, og derfor teller jeg aldri 0-ene før helt på slutten når jeg skal sette sammen den ferdige summen, ettersom jeg alltid er klar over hvor vidt sifferet som kommer før det tilhører enerplassen eller tierplassen osv.
Dersom det er mange tall som skal pulusses sammen prøver jeg alltid å lage 10-ere først. Si at jeg skal legge sammen 3+5+4+2. Da tenker jeg først 3+2(som jeg instinktivt vet=5)+5=10 deretter setter jeg 1-eren fra tierplassen sammen med 4-eren, og får 14.
Akkurat som meg. Yuhuu. Ikke alene. 😀
27 + 48
(2+4=6)
(7+8=15)
(6|+1|5=7|5)
—————–
=75
=====
Og slik er min tankeprosess på saken. ;-P
Jeg kjørte med 30+50. Så trakk jeg fra 5, som jeg da hadde rundet opp fra 27 til 30 og 48 til 50. Hvis du skjønner hva jeg mener:)
Slik tenker jeg ; 48, 58, 68, +7 . Blir 75
60 + 15
Legger enerne i det minste tallet til det største tallet. Deretter tierne i det minste tallet til den første summen.
48 + 7 = 55
55 + 20 = 75
Tierne først 20+40=60, og plusser så på enerne 7+8=15 (60+15=75).
Reduserer til hele tiere først:
20 + 40 = 60
Deretter:
7 + 8 = 15
Som gir
60 + 15 = 75
Setter det opp i hodet slik jeg ville satt det opp på et papir.
27
+ 48
Så plusser jeg 7+8, husker på 5 og så plusser jeg 1 (som da er lagt i tillegg) + 2 + 4 og får 7.
Svaret blir da 75.
Med andre ord visualiserer jeg bare regnestykket slik jeg ville satt det opp i nattetimene på barneskolen.
Som deg. 7+8 =15 2+4 + 1 i mente = 7. altså 75 Husker regnestykke-oppsett fra skoletiden for leeeeenge siden..
Jeg så umiddelbart 15+60 ..
7+8=15
3+4=7
75
Så jeg setter det vel opp slik jeg lærte på skolen i sin tid.
20+48=68+7=75
27 + 8 + 40.
Satt og betraktet tallene ei stund; så at det ene er delelig på ni, (3×9) det andre på åtte (5×8). La ikke merke til plusstegnet.
Jeg ser 75
Jeg tar
20+40
5+5
2+3
Og så adderer jeg summen av disse
30+50 Minus 5 = 75
48+20 = 68 68+7 = 75
Tierne først 20+40 =60
Deretter fyller jeg opp 8 + 2 (fra sjueren) =70
og til slutt de siste 5 som var igjen fra sjueren =75
Runder opp til nærmeste tiere:
30+50=80
Og trekker fra de 5 jeg rundet opp med:
80-5=75
Det første som slo meg var at dette er alderen til kjæresten min og meg. Ha en fin sommer. Klem fra Tyggen (Forresten også flink i matte)
27+48 7+8=15 20+40=60 -> 60+15=75
Har en tendens til å runde opp tierne, så 30 + 50 – 5, neppe beste metode siden jeg aldri var noe god i matte, men jobbet flere år i butikk der hoderegning var nyttig.
Virker som en veldig god metode, ikke minst vet du at den funker bra i praksis!
Først ser jeg er virvar av tall og det føles som en umulighet. Deretter begynner jeg å se på fingrene. Så begynner jeg å visualisere en skolebok med tall over hverandre. Jeg gjør det altså som vi lærte på barneskolen på 80-tallet…
Hei hei. Jer er Nodas Boukovalas (35), gresk mester i hoderegning og hukommelse , bosatt i Oslo for ett år. Jeg er super flink med tallene, men ikke så flytende i norsk. Reigninger som 48+27 var alltid automatisk for meg, da var jeg 4 år gammel. Til å bli aritmetiksmester og gjøre alle slags regninger, husker jeg all 100×100 gangetabellen, 1K første primtall, logaritmer, osv. Jeg representere Hellas på internasjonale hodearitmetik konkurranser for 10 år, siden er jeg utlending. Min råd for alle dere er til å prøve å ikke bruke kalkulatoren så ofte. Hjernen vårt trenger mentalt trening også. Jeg ser ofte at så mange av dere Nordmenn går så ofte til SATS eller Fresh Fitness, for fysisk trening. Men endelig, til å unngå demens osv, er viktig til å gjøre også mentalt trening ofte (som sjakk, sudoku eller litt hoderegninger). Følge meg på Instagram (nodas1) for nyheter om tallene. Mvh , Nodas
Jeg gjør dette kjempe tungvindt på skolemetoden.
Jeg tenker 8+7 = 15 og får 5 som bakerste tall for så å regne og 4+2=6 + 1 (fra 15) og får 7 som fremste tall. Så ender jeg i 75.
27+48 =>
20+48 = 68
68+7=75
20+40+(16-1)
Regelen bør vell være å summer 1-enere først, 10-ere og eventuelt 100…
Altså 7+8(=15)+20+40=75
Hvis man plusser på noen tall så vil man se at alle andre regnemåter blir utrolig komplisert!
27+48+64+73+14
Åtte og åtte er seksten. Minus én.
Førti, femti, seksti.
Sytti.
Fem.
Jeg tenker – hvor er min kalkulator?
Regnestrategien min varierer, det kommer an på hva regnestykket er.
Denne gangen ble det
48 + 20 = 68, deretter 68 + 7 = 75.
7+8 = 15 + 20 + 40 = 75
15+60 er 75
Når jeg regner i hodet er det lettere å huske tieren mens jeg regner eneren, heller enn motsatt
27 + 48
20 + 40 = 60
dvs
27 + 40 = 67
Da gjenstår åtteren
7 er 3 under tieren, som gjør det naturlig å dele opp 8 i 3+5
=75
8+7=15
20+40=60
60+15=75
68+7
Her tar jeg 48+7=55+20=75.
Jeg tenkte:
27 + 8 = 35
35 + 40 = 75
Men ser at den 25 + 50 er ganske smart!
27+48
20+40=60
7+8=15
60+15=75
30 + 50 – 5
27+48
I hodet mitt ser jeg 27 bli flyttet direkte over 48 (altså ikke «oppover-over», men at den er gjennomsiktig over 48). Så smelter 2 med 4 og jeg får 6. Blir litt irritert når jeg ser at 7+8 blir over 10. Det blir én ting til å holde styr på, og så legger jeg et tall til på 6, altså 7 på tierplass. Den er ferdig. Så «gir» jeg 2 fra 7eren til 8, den er nå midtstilt og blir en grå null, (like svakt som da 27 var gjennomsiktig i starten), og så har jeg en enkel femmer igjen på høyre side som slås sammen mot venstre med sjueren på tierplass, den gråe nullen i midten er for svak og blir borte når dette skjer. Det finnes nok enklere måter, men det fungerte for meg gjennom skolen (har R2-matte fra vgs).
Jeg ser 20 og 40 er 60. Pluss 7 er 67. Så teller jeg de resterende 8 oppover 🙈
Jeg runder opp:
50+30=80
Så trekker jeg fra 2+3=5
Og får 75
55+20 selvsagt 🙂
«27 pluss 48 var vanskelig. 27 pluss 50 er mye lettere, det blir 77, men da har jeg tatt med to for mye, så jeg må ned på 75»
23•12=69•4=7•4•10-4=276
Jeg ser 75, dette trengs ikke regnes ut.
Hadde det stått 22387 + 22319, så hadde jeg lagt sammen de de siste først, men på to tosifrede tall?
Nørd😂
48+2+5+20=75
Ser 27+48
7+8=15 (1 i mente, husker bakerste tall, 5)
2+4+(1)=7.
75
Jeg tenker 7 + 8 = 15 + 20 + 40 = 75
20 + 40 = 60
7 + 8 = 15
60 + 15 = 75
Jeg regner slik:
Regnestykke:
27 + 48
Delt opp i hodet mitt:
Først 7+8=15 og 20+40=60+15 gir sluttsummen 75 🙂
Jeg ser 8+7+40+20 = 75.
Den japanske metoden er litt wow ved første øyekast, men ser du litt etter er det bare posisjonssystemet som synliggjøres med streker og kryss i stedet for tall. Alltid når denne trekkes frem brukes lave siffer ex 21 x 22. Men prøv å gange sammen 788 x 869 med tilhørende tieroverganger. You’re in a world of hurt!
7+8=15 samt at 20+ 40 = 60 da blir 60+ 15 = 75 🙂
Eg tenker 40+20=60 og så 60+8=80 og så 68+2+5=75
Tenker 30 + 50 = 80 og trekker så fra 3 + 2 = 5 og ender da opp med 75.
25 + 50 = 75
48+7=55+20=75
🙂
Nettopp! 😎
Runder opp til helt tall….
30+50=80
3+2=5
80-5=75
Jeg ser 30+50-5=75 😁
20 + 40 + (7 + 8) = 75
Jeg regner som på barneskolen.
7+8= 15
2+4=6
Eneren over 6 = 7
Drar ned 5, blir 75.
Nå ser jeg at andre flytter tall for å lage et femmertall, det skal jeg også begynne med.
Min metode er for avansert
7+8 = 15
2+4 = 6
6*10=60
60+15=75
60 + 15
Tenkte at 27 + 48 = 75
Det varierer noe hvordan jeg regner i hode, avhengig av hva som fremstår som enklest. I dette tilfellet enten (48 + 20) + 7 = 75, eller (50 + 30) – 5 = 75.
Jeg så umiddelbart tallet 125 minus 50 = 75
48 + 7 = 55
55 + 20 = 75
Tierne som ligger nærmest gir 30+50 = 80. Ser at 27 mangler 3 på 30 og 48 mangler to på 50, altså må det trekkes 5 fra mitt overslag = 75.
Først tenker jeg at 2+4 er 6, så blir jeg stresset over hva 7+8 er. Jeg vet hva 7+7 og 8+8 er, men klarer aldri å finne mellomtingen. Dette gjør at jeg blir så distrahert at jeg mister helt fokus på hva jeg prøver å finne svaret på. Når jeg endelig har kommet frem til 15 (etter mye sjelelig smerte), blir jeg så mye mer stresset over å ha tallene 15, 27 og 48 i hodet at jeg ikke klarer å huske at jeg allerede har løst 2+4 allerede. På det tidspunktet har jeg glemt hva jeg prøver å finne svaret på. Når jeg så husker både 6, 15, 27 og 48 ender jeg opp med et så uoverkommelig regnestykke at jeg rett og slett gir opp.
25+50
27+48=(48+2)+(27-2)=50+25=75
Tror jeg er alene om denne sære måten.
Tenkte med en gang at 3 døgn er 72 timer.
72+3=75
Fordi jeg vet at 24+48=72, også må jeg legge til de 3 jeg tok vekk fra 27 (27-24=3).
20+48
=68 + 7
= 75
Jeg så 48+7 (=55) +20 = 75
30+50-5
=75
20+40+16-1 var det som skjedde her.
27+48= (20+40) + (7+8) = 60 + 15 = 75
Da jeg så regnestykket, tenke jeg «det første tallet dobler seg, det andre øker med én». Da jeg regna det, tenkte jeg 7+8=15, 20+40=60, 60+15=75
Veldig fint hvordan hver hjerne tenker det ulikt. Jeg har ofte lurt på om alle kan være ganske gode i matte hvis de bare møter den læreren som skjønner deres måte å skjønne på.
Jeg tenkte 48+20+2+5
30+50 -3 -2 = 75
Jeg låner tre fra det andre tallet, slik:
(27 + 3) + (48 – 3) = 75
30 + 45 = 75
Det er det enkleste, syns jeg.
20+40=60+7+8=75
Min første tanke: 30+48-3=75
20+40 og 7+8
Hadde det vært si 278+483 så hadde det blitt 200+400 og 70+80 og 8+3
27 + 40 + 8
7+8=15 (da har jeg funnet «eneren»; 5)
2+4+1=7 (da har jeg funnet «tieren»; 7. 1-tallet fra forrige svaret står på «tierplassen», så da skal den inkluderes her)
Så da har jeg 7 på «tierplass» og 5 på «enerplass»; 75.
Jeg summerer slik;
27+8=35
+40=75
Er eg aleine om dette? Tok ut 3 som sams faktor, adderte 9 + 16 = 25 og vips såg eg kva det vart.
Berre at eg bomma på 48 / 3 først, så det vart jo litt flaut. Men det var det som skjedde i hovudet mitt i dag. Neste gong håpar eg at eg vel noko enklare slik de andre har gjort,
27 + 48
Tenker 20+40=60,så 7+8=15. Til slutt 60+15=75.
Summerer i hodet slik jeg lærte på skolen på papir. Altså: 27 øverst og 48 under, og summerer 7+8=15, 5 under og 1 i mente over 4+2, som blir 1+4+2=7
Som blir 75
20+48=68
68+7=75
15+60=75
Mye fine kommentarer her! Det son er litt kjedelig (fra lærerperspektiv) er at vi ikke får svar fra ‘alle’, mange gidder ikke engang lese artikkelen, andre velger å ikke svare, (eller gir opp å scrolle ned!).
30+50-5 tenkte jeg
Jeg runder alltid opp eller ned en av faktorene. Justerer tilbake etterpå. Samme ved multiplikasjon. Enklere med et rundt tall.
Her blir det:
27 + 50 – 2 = 75
Jepp! 27+50-2=75 😉
7+8
2+4+1
=75
27 + 48
20 + 40 = 60
7 + 3 = 10
8 – 3 = 5
10 + 5 = 15
60 + 15 = 75
Innså til min store skrekk at det er slik jeg alltid gjør det. Ikke rart jeg er elendig på hoderegning!
27+48
Dvs:
2+4 blir 6, dvs 60
7 og 8 blir over 10, så i hodet putter eg ein tier til på 60, som då blir 70.
(Eg stjeler tre frå åtte og gir til sju for å lage denne tieren.)
Då blir det fem igjen av åtteren.
Då blir det 70+5=75.
For meg blir dette den mest lettvinte måten å gjer dette på.
Og det er vel det som er pointen, at det skal vera lettvint.
Det er viktig å huska at me tenker annerledes, og at me har lov til det.
Det hadde vore interessant å vite om ungar tenker på nokon spesiell måte før dei lærer det på skulen, eller om det å legga samen er ein heilt fraværande evne før det blir lært.
27+40=67+8=75
60+15
20+40+7+8=75
27+48?
20+40=60
7+8=15
60+15=75
27+48=
27+3+48-3=
30+45=
75
1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
En god spøk, eller er du muigens tallblind?
20+40 + 15 = 75
Det mest logiske er jo:
27+48 = 25+50 = 75
Tenker det er håp for menneskeheten fortsatt – 340 kommentarer til en artikkel og fortsatt er ingen omtalt i negative ordelag ❤️
Så gjennom kanskje 50% av svarene uten å se min fremgangsmåte.
Ville gått:
27+40+3+rest(5) = 75
27+40 = 67 => mangler så 3 for nærmeste 10’er, legger så til resterende.
Edit:
I stand corrected;
Ser 1 som gjør det likt 🙂
20+40=60
7+8=15
60+15=75
Eg tenkte ikkje på noko som helst
30+50=80
80-5=75
27 + 48
2 + 4 = 6(0)
8 + 2 + 5 = 15
60+ 15 = 75
Selvfølge 25 + 50
20+40=60
8+7= (8+2) =10
(7-2=5) + 5 = 15
10+15=25
60+15=75
Tenkte umiddelbart 60 (20+40) + 15 (7+8) = 75
Ser fort at 25 + 50 kanskje er den enkleste varianten.
20+40=60
8+7=16
=75
Obs taste feil
20+40
8+2+5
=75
«Hva skjer i hodet ditt når du ser dette: 27 + 48 ?»
Det som skjer er at jeg scroller forbi det. Jeg vet fremdeles ikke hva svaret er.
7+8 er 15 – 20+40 er 60 = 75
Vet ikke hvordan jeg summerer, leser det som 75 uten å tenke over det….
Gir mening, jeg skriver relativt ofte oppgaven av feil eller får feil svar fordi jeg regner ut noe uten å legge merke til det. kan fint se 2+6, men skrive av 2+8 og slik få 10. Når jeg da kontrollerer oppgaven er jo alt rett, 2+8 er 10, men…
30+45=75
8+7=15,2+4=6,15+60=75
2(20) + 4(40) = 6(60)
7 – 5 = 2
8 – 5 = 3
5 + 5 = 10
2 + 3 = 5
60 + 10 = 70
70 + 5 = 75
Læreren min har fremdeles rett.
Jeg tenker alt for komplisert.
27+48
(2)7+8=35
3(5)+40=75
Jeg begynner med enerne, og beholder tieren uten å tenke så mye på den, så 27+8 føles som 7+8=35. Så legger jeg til tieren, mens eneren bare henger på, 35+40 føles som 3+4=75
7 + 7 +1 = 15
15 + 40 = 55
55 + 20 = 75
Enkelt og greit:)
27
+ 48
——
=75
(48+2) + (27-2)
50 + 25
=75
Akkurat sånn tenker jeg også. Ser ike ut som det er så mange av oss. 😀
Jeg tenker sju pluss åtte, da har vi sju pluss tre pluss fem, femten, tyve pluss førti, hva i faen er det, åh, nei, enklere, førti pluss femten, det er femti fem, pluss tyve, det blir syttifem.
27+48 =>
8 + 7 = 15
40 + 20 = ??
40 + 15 = 55
55 + 20 = 75
27+48
2+4=6 altså 60
8+7=blir for vanskelig så da må jeg gjøre om til 10+5=15
60+15=75
7+8
2+4+1
=75
Tiere og enere for seg; 60+15
Nesten likt som meg, men jeg flytter 3 fra 48 til 27, i stedet for å flytte 2 fra 27 til 48. 30+45 = 75. Hoderegningsstrategier er veldig fascinerende, og også viktige. Selv om man alltid har kalkulator tilgjengelig nå, så er det veldig bra for tallforståelsen å kunne litt hoderegning. Hilsen mattelæreren
Jeg ser et regnestykket, og vurderer om jeg skal løse det eller ikke. I vurderingen funderer jeg på hva den som la ut oppgaven vil.
Deretter konkluderer jeg at matte er gøy og jeg uansett vil løse oppgaven.
Videre vurderer jeg om jeg skal løse den skolerett. Vi lærte at regnestykker skulle løses ved å begynne med med «enerplassene» og gå bakover. Denne metoden egner seg ikke for hukommelsen min ettersom jeg da må huske tallet 15 imens jeg regner ut det andre.
Dermed tar jeg 2+4=6 og vurderer hvordan jeg skal huske tallet 15. Jeg tar 6+1, husker tallet 7 og regner ut 7+8 samtidig som jeg ignorerer 1 tallet. Dermed får jeg 75 og har nesten skrevet en artikkel.
Tar ofte enerne først
15+20+40=75
20+40 =60
7+8=15
60+15 = 75
20 + 40 = 60
60 + 8 = 68
68 + 7 – 5 = 70
70 + 5 = 75
Jeg ser 27+48
7+8=(1)5
2+4+1=7
75
27 + 48 = 60 + 15 = 75
Tierne (20+40) + Enerne (7+8)
27+48
20+40=60
7+8=15
27+40=67
67+8=75
27+48:
20+40 = 60
7+7+1 = 15
60+15 = 75
jeg ser 77-2=75,kanskje jeg ser 75 hårfint før jeg ser 77-2
7 + 8 + 20 + 40
Jeg tenkte umiddelbart at her var det skikkelig stor aldersforskjell. 21år