Mens min datter og jeg sitter på flyet hjem fra ferie, blar vi i det siste nummeret av TIME Magazine. Her er det en visualisering som fanger hennes interesse. Den handler om hva du mest sannsynligvis vil dø av i ulike aldersgrupper. Etter å ha svømt mye på åpent hav og bekymret seg for hai, er hun overrasket over hva som er de vanligste dødsårsakene i hennes aldersgruppe.
For hennes aldersgruppe var de mest sannsynlige årsakene:
ulykker 27%
kreft 15%
selvmord 13%
mord 5%
Men visualisering av prosenter er litt tricky og vi fikk ikke dette helt til å stemme i starten.
Som informasjonsdesigner følte jeg behov – for ikke å si plikt – til å forklare hvordan prosentene i visualiseringen forholdt seg. Det var lettere sagt enn gjort.
Kort fortalt, så forholdt prosentene seg til antallet som faktisk døde i gitte aldersgruppe. Og dette hadde vært enkelt hvis det var like mange som døde i hver aldersgruppe, men slik er det jo ikke. I rettferdighetens navn inneholdt visualiseringen også faktiske tall på antall døde per aldersgruppe, men det var fortsatt vanskelig.
Og slik er det med det å kommunisere prosenter. Det er vanskelig også for forskere, journalister og informasjonsdesignere.
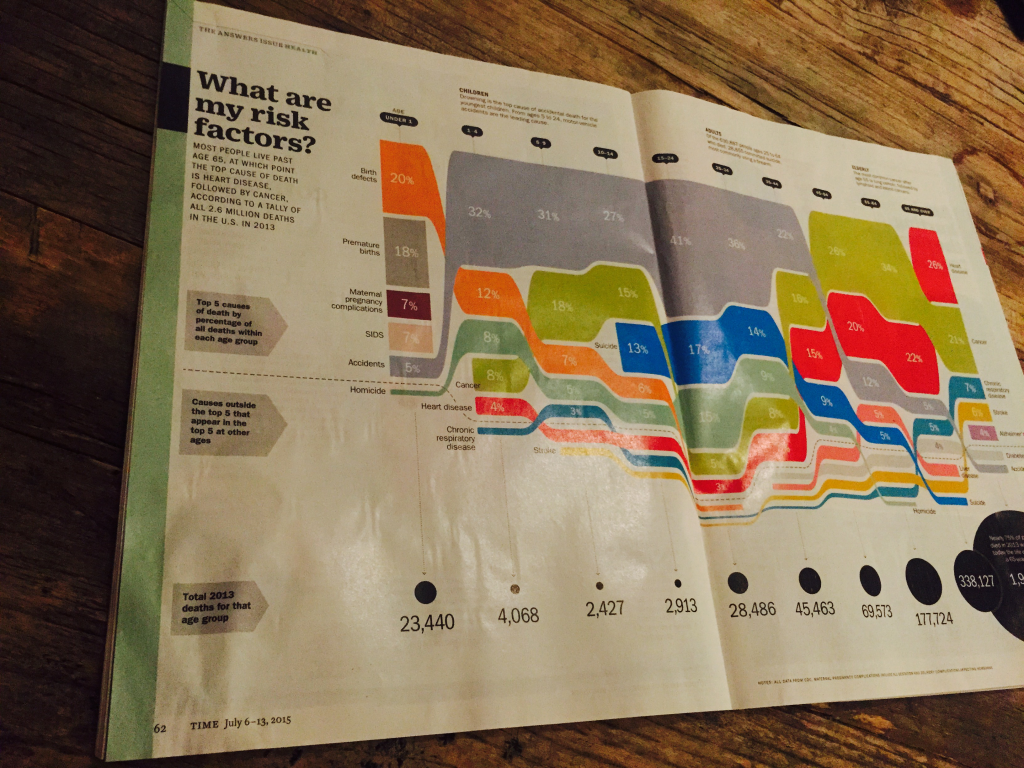
Vurdering av risiko
Professor Gerd Gigerenzer har spesialisert seg i hvordan vi oppfatter risiko, og har noen gode forklaringer på hvorfor vi sliter med å forstå risiko i prosent. Kort fortalt handler det om en værmelder som melder om 30% sjanse for regn i morgen.
Her er noen av forklaringene han har fått på utsagnet.
- Det betyr at det vil regne 30% av dagen i morgen (ca. 7 timer)
- Det betyr at det vil regne i ca 30% av regionen i morgen
- Det betyr at 3 av 10 metrologer mener at det vil regne i morgen
Alle disse forklaringsforsøkene over er gale, men viser at mange av oss har problemer med å vurdere risiko i prosent.
Det å bli litt våt er ikke så farlig, men problemet oppstår når den samme formidlingsformen brukes innenfor helse og medisin.
I dette TEDX-foredraget forteller Gigerenzer en tragisk historie fra det britiske helsevesenet og media, hvor de kommuniserer faren for blodpropp hvis du bruker p-pille.
Hva betyr «dobbelt så mange»?
I store skrifttyper skrives det at hvis du tar en tredjegenerasjons p-pille, har du dobbelt så stor sjanse for å få blodpropp. Verre kan det vel knapt bli – det er 100% økt risiko for blodpropp hvis du bruker tredje generasjons p-pille. Mange ble redde og sluttet med p-pille, som førte til økning i aborter og uønskede graviditeter. Mange fikk sine liv dramatisk endret på grunn av dette.
Forskningsrapporten media baserer seg på skriver riktignok at risikoen for blodpropp dobles. Men de skriver også at den økes fra 1 av 7000 til 2 av 7000 som sannsynligvis vil få blodpropp som følge av bruk av tredje generasjons p-pille. Dette poengteres ikke i media, og folk klarer ikke å forstå den reelle risikoen når den kommuniseres i prosentvis økning.
Her er et helt ferskt eksempel fra The Telegraph i mai, 2015: Newer contraceptive pills raise risk of blood clot four fold
Mange journalister synes nok denne er helt innenfor, da det i slutten av artikkelen blir gitt rom til flere syn på saken. Men hvilket etterlatt inntrykk tror du en tenåringsfar sitter med etter å ha lest denne, og tror du alle forstår den reelle risikoen? Er den godt nok forklart?
Hva dør folk av i Norge?
Tilbake på jobb etter ferien klarer jeg ikke helt å få visualiseringen fra TIME Magazine ut av hodet. Den er ikke helt rettferdig i måten den kommuniserer tallene på. Samtidig skjønner jeg veldig godt hvorfor de visualiserte det slik. Å visualisere store mengder (mange som dør gamle) sammen med mindre mengder (få som dør unge), hvor det også er interessante variasjoner i de små mengdene, kommer vi alltid til å slite med. Det er en knallgod faglig utfordring.
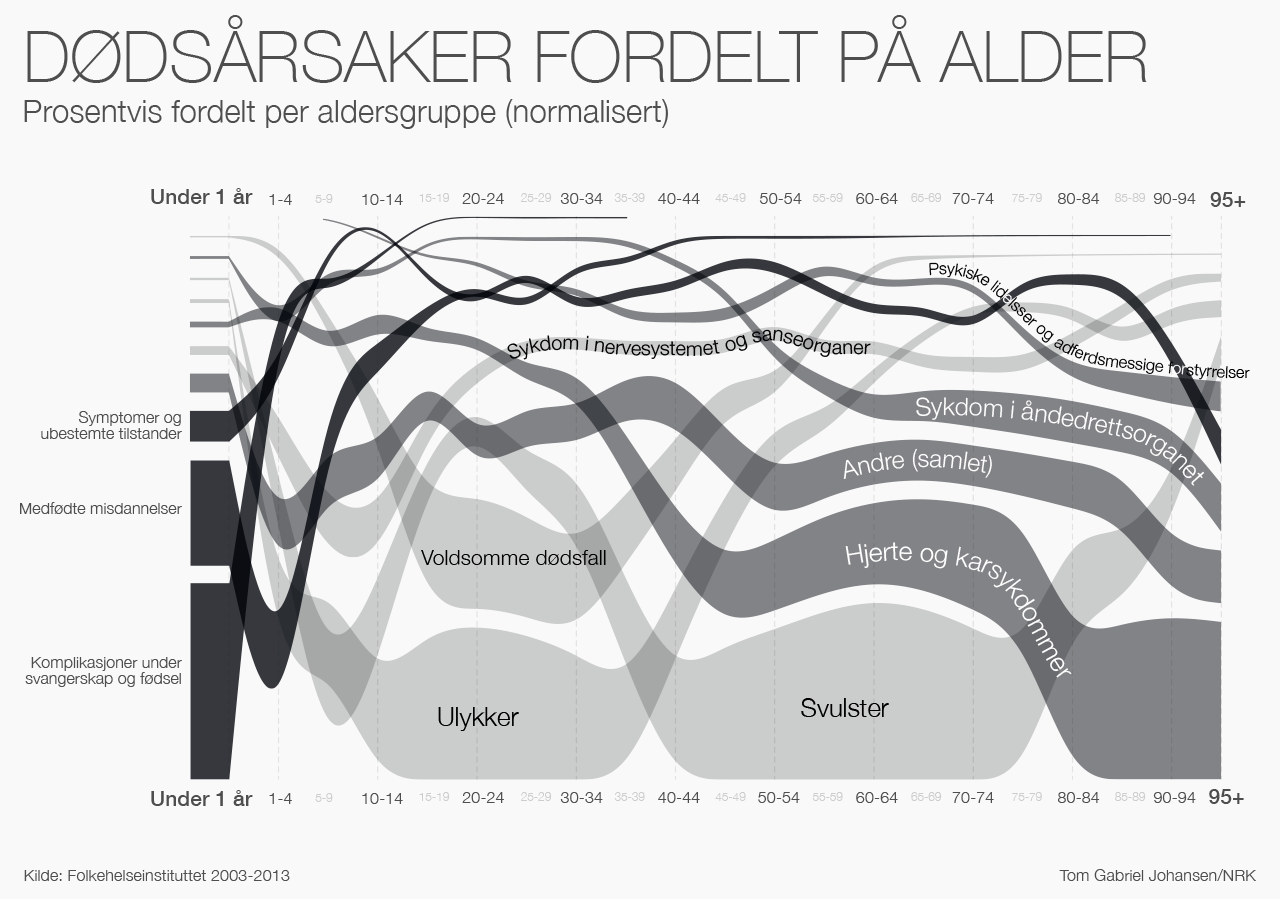
De norske tallene ser slik ut i en tilsvarende visualisering (basert på dødsfall 2003-2013). Heldigvis er det ikke like mange mord i Norge som i USA, så det ser man rett og slett ikke i den norske visualiseringen. Dødsårsakene fra Folkehelseinstituttet er litt forenklet, og jeg har slått sammen små variabler (de mindre dødsårsakene) for enkelhets skyld. Mer om dette i bunnen av denne posten.
Når vi normaliserer tallene i visualiseringen over, så gir den innblikk selv i aldersgrupper med lave dødstall, men den gir ikke et helt rettferdig bilde, så jeg har lagt ved en til. Her visualiserer jeg de absolutte tallene, som viser det helt naturlige, nemlig at folk stort sett dør når de er gamle og risikoen for å dø som ung er svært liten.
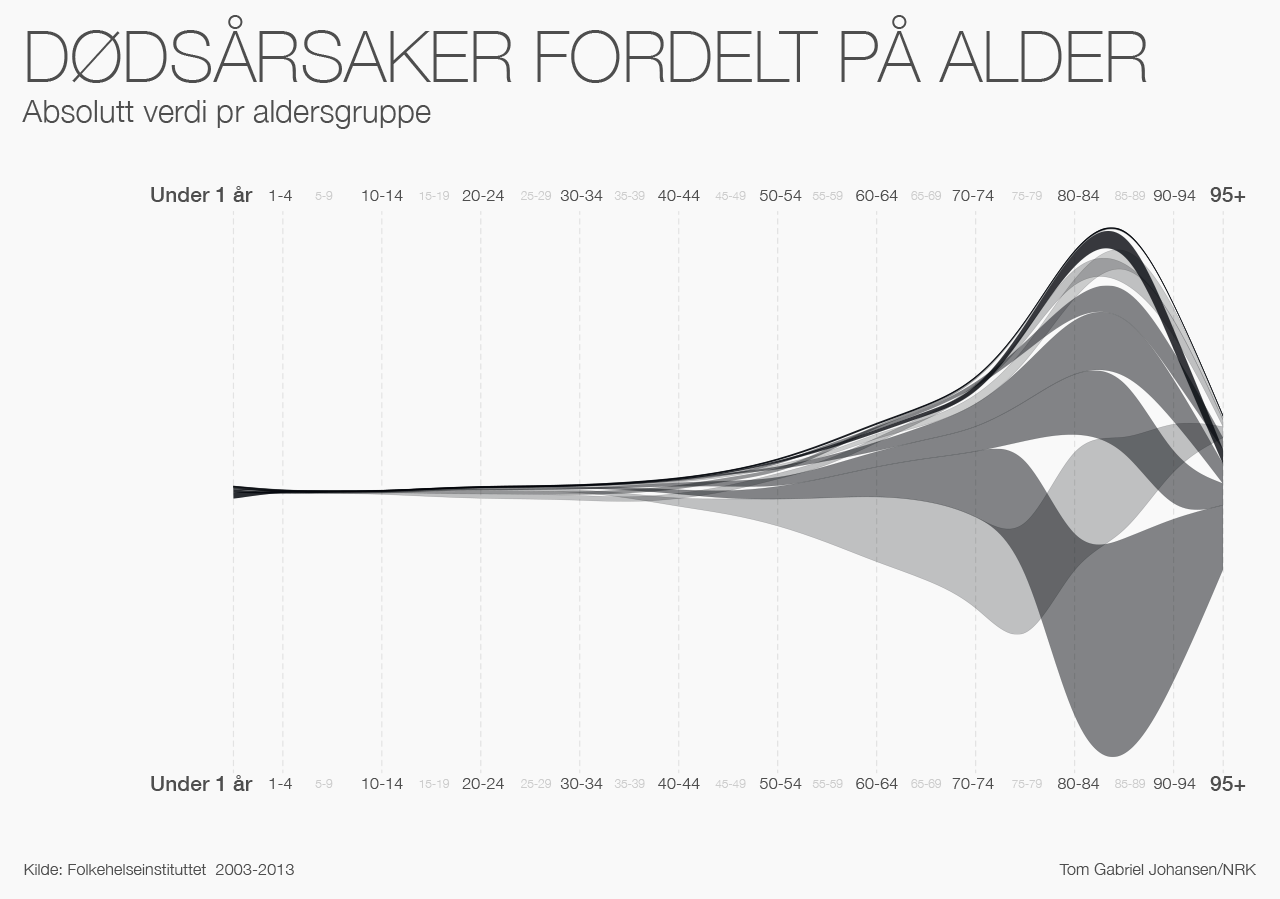
Datagrunnlaget for visualiseringene over er hentet fra Folkehelseinstituttet. Det er gjort forenklinger av navn på variabler og en del variabler er slått sammen for å forenkle det visuelle uttrykket. I variabelen ‘Andre’ ligger det flere årsaker som alene ble for små. Variabelen ‘Voldsomme dødsfall’ er slått sammen av ‘Voldsomme dødsfall’ + ‘Andre voldsomme dødsfall’. Variabelen ‘Komplikasjoner under svangerskap og fødsel’ er slått sammen av ‘Komplikasjoner ved svangerskap, fødsel, barsel (O00-O99)’ + ‘Visse tilstander som oppstår i perinatalperioden (P00-P96)’.
Det er mer informasjon rundt definisjonen av variabler på Folkehelseinstituttet
Spist av hai
Og til slutt: Frykten for å bli spist av hai i ferien var høyst reell for min datter. Men risikoen for at det skulle skje viste seg å være veldig liten. Haien ble i samme magasin rangert som det minst farlige av de skumle dyrene, med kun 3 spiste personer i hele 2014. Men hvordan frykt og reell risiko henger sammen skal vi se mer på i en annen post.
I mellomtiden kan du jo skrive en kommentar her om hvordan du forstår utsagnet «det er 30% sjanse for regn imorgen» 🙂

Prosentregning og sjansen for at slike ting kan skje, kan man aldri være sikre på.
Selv om det er minimalt med sjanse for å bli spist av hai, kan det hende at MAN SELV er den svært sjeldne som blir spist av hai. Det kan skje når som helst og hvor som helst.
Har aldri likt slik en tankemåte.
Du kan påvirke risikoen for å bli spist av en hai ganske mye. For det første må du befinne deg i sjøen, og for det andre må det finnes menneskespisende haier i samme farvann. Det skjer ikke hvor som helst eller når som helst.
Man kan ikke bli spist av hai hvor som helst. Man blir ikke spist av hai i skogen
Du kan ikke ha sett dokumentaren Sharknado.
Hai kan spise deg hvor som helst, når som helst: youtube.com/watch?v=M-pXDoe5a0E (Traileren til Sharknado, en film der det regner haier)
Relativt lave sjanser for å bli spist av hai på Hardangervidda, har jeg hørt.
Jeg forstår det som at det gitt forutsetningene når man prøver å forutse været (hvor det er høytrykk, hvor det er lavtrykk og andre relevante faktorer), vil regne på det aktuelle området 3 av 10 ganger.
Dvs. at hvis man kunne reprodusert forutsetningene nøyaktig og så latt været utviklet seg så ville det begynne å regne 3 av 10 ganger.
Når værmelderen refererer til 30% sjanse, altså 30% sannsynlighet. Det avgjørende blir da hvordan man forstår sannsynlighetsbegrepet. En definisjon på sannsynlighet er et uttrykk for frekvensen av en hendelse. Dvs. hvor ofte inntreffer akkurat den hendelsen, sammenlignet med alle andre hendelser.
Hvis værmelderen ser på historiske data at over de siste x årene at det har regnet i 3 av 10 tilfeller når værforholdene er som i dag, da kan han med rimelighet anta at det også i dag kan regne. Men han kan ikke si med sikkerhet at det vil regne. I 7 av 10 tilfeller regnet det jo ikke i de historiske dataene. Det det egentlig betyr er at hvis man ser tilbake, så var det omtrent 30% av slike dager som i dag som ga regn.
Prosenter er egentlig skumle greier. En dobling fra 1 tilfelle til 2 tilfeller er 100% økning. Massivt! Men om sannsynligheten i utgangspunktet var bare 1 av 10000, så er 2 av 10000 fortsatt veldig lavt. Fra 0,0001 % sannsynlighet til 0,0002% sannsynlighet.
Jeg forstår godt hvorfor det er fristende for journalistene å rapportere 100% økning i stedet for at sannsynligheten har endret seg fra 0,0001% til 0,0002%. Det siste ser jo mye mer skummelt ut, og generer nok flere klikk og lesere.
Samtidig, for den ekstra personen av 10000 som får sykdommen, så er det jo faktisk svært alvorlig.
Ja, prosenter er skumle.
1 av 100 er 1 %.
1 av 10 000 er 0,01 %.
1 av 1 000 000 er 0,0001 %
Poenget ditt holder fortsatt vann, selv om prosentregningen ikke gjør det.
Upsda! Noe så flaut. Glemte å gange med 100. her gjør jeg et poeng om å ikke overdrive, og så underdriver jeg i stedet. Takk for opprettingen!
30% sjanse for regn i morgen, må vel tolkes som at det er en relativt liten sjanse for regn, ettersom det er 70 % sjanse for at det ikke vil regne. (Om du ikke bor i Bergen da. Her er 30% så godt om garanti for at det kommer regn.)
Det kan vel videre tolkes som meteorologens «sikkerhetsmargin». Altså; skulle det regne, noe som det er liten risiko for, har han tross alt tatt høyde for det, og har derved dekning for sitt varsel.
Jeg tolker det også slik. I tillegg er det og viktig å spesifisere hva regn er. Er det regn hele dagen? Vanligvis så vil slike utsagn vise til hvordan været er kl 12 den dagen, det er det værsymbolene for en hel dag viser, ikke «gjennomsnittet» av dagen slik kanskje mange tror.
Hvis du har 2 modeller, A og B, der A gir at det regner og B gir at det ikke regner, så har de slikt regnet seg frem til at modell A er riktig 3 av 10 ganger.
Er du sikker på at det er kl 12, og ikke sannsynligheten for at en gitt mengde nedbør faller i løpet av de 24 timene varselet gjelder for?
Jeg har i alle fall alltid tolket dette som at det er 70% sjanse for ikke noe regn, og hvis det f.eks også er sagt 0,5mm så er det dermed kun 30% sjanse for at ca 0,5mm regn faller.
Dette innebærer i så fall at det er svært lite sannsynlig for regn akkurat kl 12.
Den dumme delen av hjernen min tenker at det er 50 % sjanse for både regn og at man blir spist av hai. For enten skjer det, eller så skjer det ikke. To mulige utfall, altså fifty-fifty. Men den smarte delen av hjernen skjønner jo at dette ikke stemmer. (Men likevel …)
He he – den tror jeg mange kjenner seg igjen i Mats.
Boktips: nytimes.com/2011/11/27/books/review/thinking-fast-and-slow-by-daniel-kahneman-book-review.html
Veldig interessant tema og godt skrevet. Bra!
Takk Evy 🙂
Jeg leste engang: The lotteri is stupidtax for the induvidual»men vell så sant er det at statistikk er irrelevant for individet.
Statistikk er et godt verktøy om du sitter på den siden som skal kostnadsberegne o.l., men om det renger i morgen vet vi ikke før i morgen…..
Tore
Har fått en del spørsmål om forskjellen på ‘Voldsomme dødsfall’ og ‘Ulykker’. Og det skjønner jeg godt.
Dette er hva definisjonene er i statistikkbanken til Folkehelseinstituttet.
Voldsomme dødsfall (Andre voldsomme dødsfall)
Selvmord, villet egenskade (X60-X84, Y870)
Drap (X85-Y09, Y871)
Skade, uvisst om påført med hensikt (Y10-Y34, Y872)
Voldsomme dødsfall (andre) (V01-Y89)
Ulykker
Ulykker Transportulykker (V01-V99, Y85)
Fallulykker (W00-W19)
Forgiftningsulykker (X40-X49)
Ulykker (andre) (V01-X59, Y86-Y86)
Her er en lenke til Statistikkbanken deres: statistikkbank.fhi.no/dar/
Spennende fremstilling av kompekst materiale. I det du beskriver de ulike variabelene, er det en ting som slår meg: Risikoen for feil i datagrunnlaget. Eksempelvis: Bil kjører ut av veien, registreres som transportulykke, mens kan hende var dødsfallet villet. Dødsårsak blir fort klassifisert ut i fra den avdødes livssituasjon og alder og små feil har stor betydning i aldersgrupper med liten «dødelighet».
Håvard: «Spennende fremstilling av kompekst materiale. I det du beskriver de ulike variabelene, er det en ting som slår meg: Risikoen for feil i datagrunnlaget. Dødsårsak blir fort klassifisert ut i fra den avdødes livssituasjon og alder og små feil har stor betydning i aldersgrupper med liten “dødelighet”.»
Nå er du inne på en annen ting. For et par år siden leste jeg noe om at det er veldig få standardmessige obduksjoner som blir utført i Norge – nok av forskjellige årsaker, som at vi har relativt få drap.
1 Er det noen som kan si noe om dette?
2 Hvor sannsynlig er det at en dødsårsak kan være feil, som resultat av manglende obduksjon?
Jeg anbefaler deg å lese om obduksjoner i Tidsskrift for Den norske legeforening, aka. «Tidsskriftet»
tidsskriftet.no/articlesearch?q=obduksjon&source=mosez
Hei Håvard
Jeg var inne på samme tanke når jeg bearbeidet datagrunnlaget for visualiseringene. Det var derfor jeg valgte å ta et tiårs utvalg (2003-2013), så data grunnlaget ble litt mer solid. Men fortsatt ganske sårbart for feil.
Dette er også litt av grunnen til at jeg ikke tok med det eksakte antall (y-aksen), men ville at det skulle fokuseres på trender og utvikling i datamaterialet.
Tidlig i prosessen ville jeg gjerne ha med usikkerhets graden i visualiseringen, men fant ingen gode parameter jeg kunne bruke. Men jeg fant denne som forteller litt om arbeidet som gjøres for å forbedre innrapporteringen. tidsskriftet.no/article/3323508
Artikkelen fra tidskriftet underbygger din misstanke om sannsynlighet for feil i datagrunnlaget.
Sannsynligheten for regn er betinget den informasjonen man innehar når beregningen foretas. Så hvis vi befinner oss i en sort boks, fullstendig avgrenset fra omgivelsene, og vi blir spurt «hva er sannsynligheten for at det kommer til å regne i morgen» bør svaret være 50%. Vi har to tilstander som kan forekomme – regn eller ikke regn – hvor sistnevnte ikke nødvendigvis innebærer at det er strålende sol hele dagen, men bare at det, nettopp, ikke regner. Videre kan vi definere utsagnet «regne i morgen» til å bety at det på et eller annet tidspunkt vil regne, uten å videre definere om det kommer til å regne mye eller lite, i 5 minutter eller 5 timer.
Dette vil være normaltilstanden – 50% sannsynlighet, ikke 0% som er mer naturlig/intuitivt å tenke. Men meteorologene sitter ikke i en sort boks og gjør betraktningene sine, de har tilgang på store mengder data og matematiske beregninger, noe som påvirker sannsynligheten. Hvorvidt det kommer til å regne i morgen eller ikke er avhengig av denne informasjonen. Så når meteorologene sier at det er 30 % sannsynlighet for regn i morgen, sier de egentlig én av to ting:
1. «Vi har informasjon som reduserer sannsynligheten for regn i morgen, men denne informasjonen utelukker ikke regn» (=> noe i dataene tyder på regn)
2. «Vi har informasjon som reduserer sannsynligheten for regn i morgen, men vi har ikke nok informasjon til å utelukke regn» (=> sikkerhetsmargin)
Jo nærmere i tid man kommer, jo mer informasjon sitter man på og det reduserer feilmarginen i utsagnene. Hvis klokken er 23 på den aktuelle «morgendagen», det har ikke regnet hele dagen og himmelen er skyfri, vil de fleste si at sannsynligheten er svært lav for at det kommer til å regne denne dagen samt at det er lite usikkerhet knyttet til det utsagnet.
Denne forskjellen på sannsynlighet og usikkerhet er det nok mange, journalister som lesere, som ikke er bevisst på.
Du har et lite hull i resonnementet ditt. Selv om det er to hendelser, trenger ikke sannsynlighetsfordelingen å være uniform, altså at det er like stor sjanse for begge hendelsene. Det er fristende å tenke sånn, men om værsystemet virkelig er en svart boks er det en ukjent sannsynlighet.
Til det opprinnelige spørsmålet: For å finne denne sannsynligheten, er det nødvendig med sampling — tilfeldig utvalg fra den svarte boksen — og det er her mine spekulasjoner begynner. Værendringer er en kaotisk prosess, og en liten endring i forutsetningene kan føre til store endringer i resultatet. Det kan man nok utligne noe ved å prøve mange forskjellige små variasjoner i forutsetningene før man regner på dem. 30 % sjanse for regn vil da tilsvare at 30 % av simuleringene hadde nedbør, og at hver av simuleringene er like sannsynlige.
Hvis fordelingen av simuleringene ikke er uniform, kan man komme fram til en endelige sjansen ved å slå sammen regnhyppigheten i simuleringene og sannsynlighetsfordelingen på dem.
Det kommer helt an på hva man skal. Hvis planen er motorsykkeltur, eller varselet gjelder for 17 mai, ja da er 30% sjanse for regn nærmest en garanti for at det vil regne. Hvis du er bonde og trenger regn, ja da blir det nesten helt sikkert opphold. Problemet oppstår dersom bonden også har tenkt seg på motorsykkeltur på 17 mai.
Da blir det nok overveiene regnvær, ikke noe på jordet.
Et interessant poeng er at om vi overfører sannsynlighetene til oppslutning om partier i meningsmålinger og valg har folk mye mindre problemer med å forstå hva det dreier seg om. Om parti A går fram fra 2% til 4% er dette selvsagt en økning for dette partiet med 100%, men folk forstår likevel at dette betyr lite all den tid det er prosentandelen til dette partiet som del av totalen for alle partiene som teller. De som arbeider med analyser av valg bruker derfor «prosentpoeng» for å beskrive endringer i den relative andelen vis-a-vis andre utfall (les oppslutningen om andre partier).
Lek med tall og statestikk i forhold til sannsynlighet kan være farlig om ikke grunnlagsmateriale er godt og stort nok. Et eksempel: i nyere tid er det to stykker som har falt ned fra snøskavelen på nordsiden på Glitretind. En omkom og en overlevde (utrolig nok) i følge statestiken er det da 50% sjanse for å overleve et fall ned nordveggen. Jeg ville ikke satset på det!
Hei Torkjell
Jeg tror nok at deler av datagrunnlaget fra Dødsårsaksregisteret kan være litt tynt av flere grunner. At grunnlaget (antallet) kan være veldig lite + at det vist nok er en komplisert innmeldingsprosess av dødsfall. Ref: tidsskriftet.no/article/3323508
Det var et beviste valg å visualisere den akkurat slik for å fremheve trender og utvikling og ikke helt nøyaktige verdier, for rett og slett å fokusere på den litt større kroppen av datagrunnlaget.
Enig med deg at dette er viktig og jeg savner ofte en kommentar/veiledning fra organisasjoner som leverer statistikk, om hvor sikkert datagrunnlaget egentlig er.
1/3 sjanse for at det blir regn, men 2/3 sjanse for at det ikke kommer regn.
Artikkelen er svært interessant, og forklarer og illustrerer på en god måte hvor vanskelig det er å forklare og presentere data. Dessverre blandes begrepene i artikkelen. Risiko brukes som synonym for sannsynlighet. Dette er en vanlig feil. Risiko er ikke det samme som sannsynlighet, men derimot produktet av sannsynligheten for en hendelse og konsekvensen av hendelsen. Dersom en hendelse er sannsynlig og konsekvensen av den er liten blir risikoen liten. Derimot har en hendelse med liten sannsynlighet og svært stor konsekvens – f.eks. død – stor risiko.
Sannsynligheten for å bli spist av hai er liten, svært liten. Konsekvensen er uendelig stor, død. Dermed er risikoen stor.
Sannsynligheten for å dø som ung er liten. Risikoen er stor i og med at konsekvensen er fatal (uendelig stor).
Hei Kåre
Du har helt rett. Uttrykkene ‘sannsynlighet’ og ‘risiko’ er blandet i posten og det er forvirrende. Vi hadde en diskusjon på dette rett etter publisering i dag og jeg beit meg i leppa da jeg oppdaget det.
Kommentaren din er viktig og belyser problemet med forvekslingen så bra, at jeg jeg tar den med i en eventuell revidering av posten.
En av årsakene til forvirringen ved bruken av sannsynligheter/sjangs og risiko er at det eksisterer flere ulike definisjoner av begrepene.
Hvis jeg tolker 30 % sjangs som 30 % sannsynlighet (for regn imorgen) er tolkningen min avhengig av hvilken definisjon av sannsynlighet som anvendes. Frekvensfortolket og subjektive sannsynligheter er de mest brukte:
Frekvensfortolket: «Andelen ganger det regner imorgen når situasjonen repeteres et uendelig(hypotetisk) antall ganger under lignende forhold» = 30 %
Denne definisjonen gir imidlertid lite mening da vi må introdusere en uendelig (hypotetisk) populasjon av lignende situasjoner for å definere den frekvensfortolkede sannsynligheten for regn imorgen.
Subjektiv sannsynlighet: P(Regn imorgen|K) = 30%, hvor K betegner angiverens kunnskap i form av forutsetninger og antakelser, forenklinger, modeller etc. Den subjektive sannsynligheten uttrykker angiverens usikkerhet/grad av tro for hvorvidt det vil regne i morgen, betinget på angiverens kunnskap K. Forskjellige personer har ulik kunnskap (K), noe som gir opphav til ulike angivelser av sannsynligheter for den samme hendelsen (etc regn imorgen).
Aktiviteten «å trekke en bestemt ball ut av en urne» brukes ofte for å forklare/uttrykke angiverens grad av tro/usikkerhet. Utsagnet «30 % sjangs for regn imorgen» kan dermed sammenlignes med aktiviteten å trekke en hvit ball ut av en urne som inneholder 30 hvite baller og 70 blå baller. Usikkerheten/graden av tro er den samme i de to tilfellene.
Sannsynligheter defineres normalt som en av disse to kategoriene. Det finnes imidlertid et stort antall definisjoner av risiko. Risiko definert som produktet av sannsynlighet og konsekvens brukes imidlertid mindre og mindre på grunn av svakheter i presentasjon/forklaringen av risiko. Dette er hovedsaklig på grunn av at hendelser med høy sannsynlighet og «liten» konsekvens ikke kan skilles fra hendelser med lav sannsynlighet og «ekstrem» konsekvens selv om de to situasjonene helt klart er ulike (og krever ulik behandling)
«Risiko definert som produktet av sannsynlighet og konsekvens brukes imidlertid mindre og mindre på grunn av svakheter i presentasjon/forklaringen av risiko».
Dette er ikke helt rett. En risiko er en vurdering – av hvor stor/liten sannsynlighet det det er for at en hendelse skal inntreffe, og konsekvensene dersom den inntreffer. Når risiko uttrykkes som et objektivt tall, f.eks. sannsynlighet multiplisert med konsekvens kan det ikke skilles mellom hendelser med høy sannsynlighet og liten konsekvens, og hendelser med lav sannsynlighet og stor konsekvens. Derfor brukes det ofte matriser i fremstillingen av risiko. Problemet med matriser (estimeringen av sannsynlighet) er at de ikke får frem usikkerheten.
Risiko kan ofte ikke betraktes som et objektivt tall. En risiko er en vurdering – av konsekvensene en mulig fremtidig hendelse kan medføre.
Flott at det ryddes i begrepsbruken! 🙂
Takk for et flott arbeid. I mitt mangeårige liv som samfunns-forsker har jeg måttet rydde opp i mange feilfortolkninger av sannsynlighetsanalyse og risikofaktorer, også på høyt nivå i samfunnet.
Det er en begrensende side ved dataene dine du ikke sier noe om, og som i mange tilfelle kan innebære alvorlige problemer om du ikke holder tunga i rett munn, 😉 når du tolker dataene.
Du tar grunnleggende sett utgangspunkt i ti kohorter av dødstilfelle og presenterer de grafisk i et tenkt livsløp. Dette livsløpet er en konstruksjon – gitt dataene – og ikke en statistisk aggregering av faktiske (historiske) livsløp.
Figuren fører lett til feilfortolkningen at det leses som sannsynlig dødsårsak ved den angitte fysiske alder av et «gjennomsnittlig» livsløp. Det er ikke det de sier! De forteller om sannsynlig dødsårsak ved gitt alder i perioden 2003-2013 – og den sammenligner dermed mellom forskjellige livsløp. Det er en inter-kohort variasjon som da blir borte.
Om dataene dine kan si noe om forventede dødsårsaker som funksjon av levd alder avhenger da av om disse inter-kohort-variasjonene er neglisjerbare eller ikke. For mange av dødsårsakene vil jeg tro at de ikke er neglisjerbare, ikke minst på grunn av et stort medisinsk framskritt – bl.a. på tidlig diagnostisering av genetisk betingede sjukdommer, svangerskaps- og fødselsmedisin osv. – i det siste hundreåret. Du har individer på venstre side i datasettet som født i 2013, og du har individer mot høyre som er født i 1908 og før.
Om disse inter-kohortale(?) variasjonene kan neglisjeres er da å stille to spørsmål (1) har spektret av dødsårsaker historisk har endret seg med sosial eller historisk tid, og (2) kan det forventes å endre seg i framtida. Jo raskere disse endringen er, jo mindre sier dataene om endringer i forventningene over et gitt eller en gruppe livsløp.
Til de av oss som lever av å formidle innsikt basert på statistiske data:
Du er alltid en slave av historiske data på denne måten når du danner deg forventninger og gjør risikoanalyse som dette. Dette er derfor også en vurdering du alltid må gjøre når du presenterer data som dette.
Men takk for et meget godt forsøk. Og et svært godt formidlet budskap.
Alt godt,
Johan
PS:
NB! Jeg sier ikke at du ikke er klar over dette. Tvert i mot viser du med din datters helt korrekte spørsmålsstilling:
«Etter å ha svømt mye på åpent hav og bekymret seg for hai, er hun overrasket over hva som er de vanligste dødsårsakene i hennes aldersgruppe.» (min utheving)
at selv din datter er klar over aldersgruppevariasjonen! 😉 Det antyder en framifrå oppdragelse.
Men jeg mente det var et poeng som fortjente å bli uttrykt direkte og eksplisitt.
Hei Johan!
Og takk for en veldig innsiktsfull kommentar.
Du peker på noe jeg slet med i starten av prosjektet. Jeg ønsket at visualiseringen skulle si noe om forventninger og risiko, men skjønte raskt at jeg aldri selv ville evne å vekte grunnlaget og ta hensyn til historiske eller fremtidige endringer/premisser. Så jeg brukte aldri ordet risiko i diagrammet med vilje slik som Times Magazine gjorde, og innfant meg med å bare vise hva folk døde av i den gitte tiårsperioden.
Men innspillet ditt er like gyldig for det. Når man ser visualiseringen i kontekst av posten som handler mye om sannsynlighet og risiko, så ble mitt kompromi at noen vil tillegge visualiseringen mer egenskaper enn det den egentlig har. Hovedpoenget som jeg forsøkte å få frem var at en normalisert visualisering er god å ha for den engasjerer og viser variasjonen i de små tallene, men den er svak når du skal vise sammenhengen mellom de store og små tallene. Og dette er fortsatt en uløst faglig utfordring, som jeg håper å kunne jobbe mer med fremover.
Kommentaren din synes jeg er viktig og vil gjerne vite om du vet om tallmaterialet som tar opp i seg forholdene du nevner? Dødsårsaker er neppe noe som vil gå av mote med det første, så en god (les mer riktig) visualiseringen av dette hadde vært flott.
Min datter er nok dessverre litt belastet med visualisering og statistikk, da hun ofte har vært min adopterte bruker/leser i mange prosjekter 😀
Tegneserieartisten Randall Munroe har et godt poeng som er verdt å ta med seg i forhold til at man skal ikke blindt stole på statistikk i forhold til å vurdrere hvor farlig ting er:
xkcd.com/795/
Opplevd risiko og fare er stort sett voldsomt avvikende fra reell risiko og fare og henger stort sett sammen med voldsomheten som oppleves.
Det er ingen jeg kjenner som tenker to ganger over det å gå over veien eller sette seg i bilen og kjøre til jobb eller på butikken, men å fly, det kjenner jeg flere som synes er farlig.
Dette skyldes nok voldsomheten i slike ulykker også. Selv om antallet enkelt-ulykker som involverer biler og bakketrafikk er langt langt høyere enn antall flyulykker så smøres enkelt-ulykker som involverer fly ut over alle førstesider på aviser, gjerne over flere dager, med sort bakgrunn og store bokstaver, fulgt av grusomme bilder.
Som enkeltperson virker det da lettere å tenke at fly er mye farligere enn å kjøre bil selv om det i realiteten er helt motsatt. Dvs. at gitt valget om å kjøre til Italia eller fly til Italia, og risiko for ulykker kun skal brukes som kriterie for å velge så ville jeg valgt å fly, langt mindre risiko for ulykker med fly på en så lang strekning.
Men samtidig, gitt scenarioet at man vil komme i en ulykke uansett hvem av de to man velger så ville jeg valgt å kjøre, man har større sjanse for å overleve i en enkelt bil-ulykke enn man har i en enkelt fly-ulykke.
Men, uansett, gitt 30% sjanse for at det regner i morgen, så tenker jeg at det er 30% sjanse for at det forekommer regn i morgen, dvs. at om det regner hele dagen, litt nå og da, eller en kort periode midt på dagen, det er alle forekomster av regn, og det er det 30% sjanse for at skjer. Det er derfor høyere sjanse for at det ikke forekommer regn. Hvis det skulle regne så kan regn være alt fra å bøtte ned til lett duskregn.
Og så synes jeg det er bedre å tenke positivt, så det er 70% sikkerhet for at det blir opphold 🙂
Avslutningsmessig: youtu.be/8gob9NlqF7A?t=41 🙂
Enig Lasse, det er ikke alltid rasjonelt hvordan vi tenker på risiko, og det er veldig spennende tema (og stort ansvar) å utforske når man jobber i media.
Kanskje den flotteste vrien på værmeldingen er 70% sannsynlighet for opphold – hvorfor melder vi ikke opphold – godt tenkt 🙂
Svaret som Gigerenzer gir er veldig enkelt. «Det vil antageligvis ikke regne i morgen.»
Takk for positiv tvist Lasse.